Basic Maths for Adults: All You Needed in School

Mathematics is a fundamental skill that plays a crucial role in our daily lives. Whether it's managing finances, cooking, or even understanding time, basic maths is everywhere. This article aims to provide a guide to basic maths for adults, covering the essential concepts in a simple, easy-to-understand manner.

As an adult, basic maths such as addition, subtraction, multiplication, and division are vital. Fractions, decimals, and percentages can help you manage your finances and make sense of discounts, while conversions are useful for things like cooking, travel, and international transactions.

You will find these basic concepts in the article below. You will also find practice questions (with answers) to try once you understand each maths principle.

Basic Maths for Adults

Fundamental Arithmetic: Addition and Subtraction

Addition and subtraction are the most basic operations in maths. They are used when we combine or separate quantities.

For example, if you have 5 apples and you buy 3 more, you would add 5 and 3 to find out you now have 8 apples. Subtraction is the opposite. If you then give 2 apples to a friend, you would subtract 2 from 8 to find out you have 6 apples left.

Practice Questions:

1. What is 7 + 5?
2. What is 16 - 9?
3. What is 23 + 14?
4. What is 45 - 21?
5. What is 32 + 8?
6. What is 63 - 47?
7. What is 12 + 18?
8. What is 72 - 19?
9. What is 50 + 25?
10. What is 80 - 32?

* You will find the answers to these questions at the end of the article.

Fundamental Arithmetic: Multiplication and Division

Multiplication is a shortcut for addition of the same number over and over again (repeated addition). If you buy 3 packs of apples, each containing 4 apples, you would multiply 3 by 4 to find out you have 12 apples.

Division is the opposite of multiplication. If you have 12 apples and want to divide them equally among 3 friends, you would divide 12 by 3 to find out each friend gets 4 apples.

Try visualising these numbers using counters. Once you a physically holding something, it is easier to divide it up equally, or multiply it. The key to understanding multipplication and division is learning your 'times tables', which you can find below.

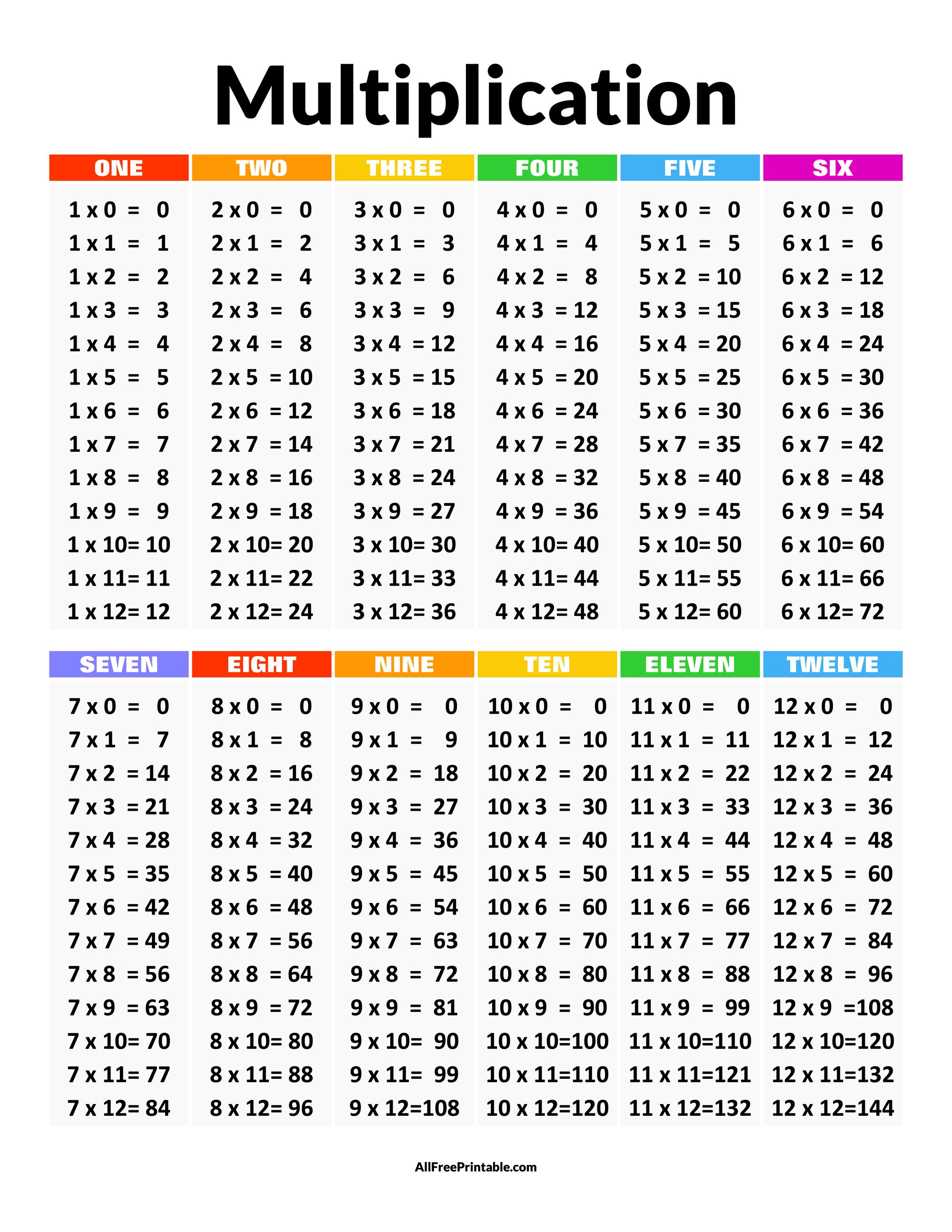
Practice Questions:

1. What is 8 x 7?
2. What is 45 ÷ 9?
3. What is 6 x 5?
4. What is 36 ÷ 6?
5. What is 9 x 7?
6. What is 81 ÷ 9?
7. What is 12 x 3?
8. What is 72 ÷ 8?
9. What is 10 x 5?
10. What is 64 ÷ 8?

Decimals and Fractions

Decimals and fractions represent parts of a whole. They are especially important when dealing with money and measurements. In order to determine the value of a fraction of something, you need to convert the fraction to a decimal (see the table below) and multiply that something by the decimal.

For example, 0.5 or 1/2 of a dollar is 50 cents. This is because 1/2 of a dollar is the same as 0.5 of a dollar. If I want the answer in cents, I need to convert the dollar to cents in my equation. Therefore, 0.5 x 100 cents = 50 cents.

Understanding how to add, subtract, multiply, and divide with decimals and fractions is a crucial skill.

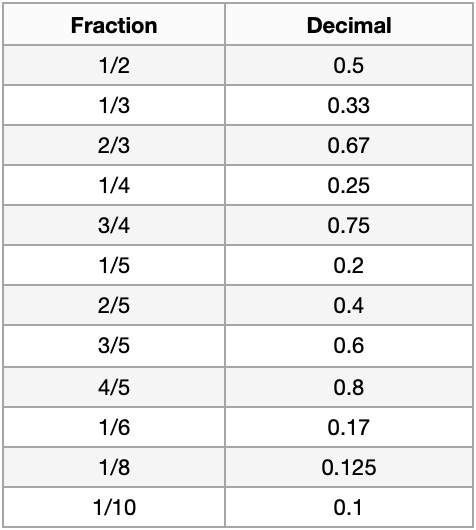
Practice Questions:

1. Convert the decimal 0.75 into a fraction.
2. Convert the fraction 3/5 into a decimal.
3. What is 0.25 + 0.50 expressed as a fraction?
4. What is 2/3 - 1/3 expressed as a decimal?

Percentages

Percentages are another way to represent parts of a whole, but out of 100. They are commonly used in sales, taxes, and interest rates. To calculate the percentage of a certain value, you can use the following formula:

  Percentage = (Part / Total) x 100

Here's a breakdown of the formula:

• Part: This is the number that you want to turn into a percentage.
• Total: This is the total or whole number.
• The multiplication by 100 is what converts the decimal number into a percentage.

For example, if you have 45 apples out of a total of 100 apples and you want to find out what percentage 45 is of 100, you would substitute the numbers into the formula as follows:

Percentage = (45 / 100) x 100 = 45%

So, 45 apples represent 45% of the total number of apples.

Practice Questions:

1. If there are 50 students in a class and 15 of them are wearing glasses, what percentage of students are wearing glasses?
2. A shirt was originally priced at $80, but is now on sale for $60. What is the percentage decrease in price?
3. You have read 125 pages of a 500-page book. What percentage of the book have you read?

Conversions

Conversions are necessary when we switch between different units of measurement. For example, converting feet to meters, or dollars to euros. This is particularly important in cooking, travel, and finance.

There are many units of measurement, but these conversions are easily done through a basic conversion calculator (such as those on Google). You can find each of these as you need them.

Understanding basic maths is not just about knowing the concepts, but also about applying them in real-life situations. Whether you're calculating a tip at a restaurant, budgeting your monthly expenses, or measuring ingredients for a recipe, basic maths is a skill that you'll use regularly.

Maths might seem intimidating at first, but with practice, it becomes second nature. Remember, everyone learns at their own pace, so don't rush. Take your time to understand each concept, practice regularly, and don't be afraid to ask for help if you need it. With patience and perseverance, you'll master basic maths in no time!

Practice Problems

To help you practice and reinforce your understanding, here are some practice problems. In these problems, you will first need to identify which maths principles you need to use, and then use that principle to find the answer!

1. If you buy 7 items each costing $3, how much do you spend in total?
2. You have $50. After buying a book for $15.75, how much money do you have left?
3. If a store offers a 30% discount on a jacket that costs $80, how much does the jacket cost after the discount?

Remember, practice makes perfect. Keep working on these basic maths skills, and you'll see improvement in no time. Happy learning!

Answers

Fundamental Arithmetic: Addition and Subtraction

1. What is 7 + 5? Answer: 12
2. What is 16 - 9? Answer: 7
3. What is 23 + 14? Answer: 37
4. What is 45 - 21? Answer: 24
5. What is 32 + 8? Answer: 40
6. What is 63 - 47? Answer: 16
7. What is 12 + 18? Answer: 30
8. What is 72 - 19? Answer: 53
9. What is 50 + 25? Answer: 75
10. What is 80 - 32? Answer: 48

Fundamental Arithmetic: Multiplication and Division

1. What is 8 x 7? Answer: 56
2. What is 45 ÷ 9? Answer: 5
3. What is 6 x 5? Answer: 30
4. What is 36 ÷ 6? Answer: 6
5. What is 9 x 7? Answer: 63
6. What is 81 ÷ 9? Answer: 9
7. What is 12 x 3? Answer: 36
8. What is 72 ÷ 8? Answer: 9
9. What is 10 x 5? Answer: 50
10. What is 64 ÷ 8? Answer: 8

Decimals and Fractions

1. Convert the decimal 0.75 into a fraction. Answer: 3/4
2. Convert the fraction 3/5 into a decimal. Answer: 0.6
3. What is 0.25 + 0.50 expressed as a fraction? Answer: 3/4
4. What is 2/3 - 1/3 expressed as a decimal? Answer: 0.33 (or 0.34 rounded to two decimal places)

Percentages

1. If there are 50 students in a class and 15 of them are wearing glasses, what percentage of students are wearing glasses? Answer: 30%
2. A shirt was originally priced at $80, but is now on sale for $60. What is the percentage decrease in price? Answer: 25%
3. You have read 125 pages of a 500-page book. What percentage of the book have you read? Answer: 25%

Practice Problems

1. If you buy 7 items each costing $3, how much do you spend in total?
   Answer: $21
2. You have $50. After buying a book for $15.75, how much money do you have left?
   Answer: $34.25
3. If a store offers a 30% discount on a jacket that costs $80, how much does the jacket cost after the discount?
   Answer: $56